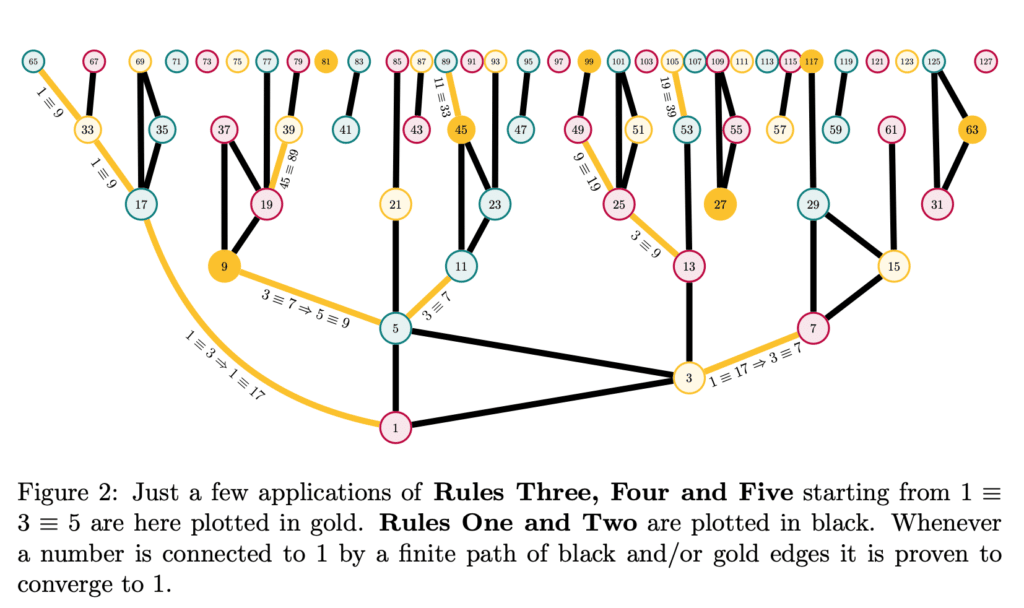
The Collatz dynamic is known to generate a complex quiver of sequences over natural numbers which inflation propensity remains so unpredictable it could be used to generate reliable proof of work algorithms for the cryptocurrency industry. Here we establish an ad hoc equivalent of modular arithmetic for Collatz sequences to automatically demonstrate the convergence of infinite quivers of numbers, based on five arithmetic rules we prove apply on the entire Collatz dynamic and which we further simulate to gain insight on their graph geometry and computational properties. We then formally demonstrate these rules define an automaton that is playing a Hydra game on the graph of undecided numbers we also prove is embedded in 24N − 7, proving that in ZFC the Collatz conjecture is true, before giving a promising direction to also prove it in Peano arithmetic.
